НИЧТОЖНЫЕ ПРОЦЕНТЫ

Сдавал в этом году ЕГЭ. Мне попалась задача: Иванов взял кредит на три года под 10% годовых с выплатой ежегодными аннуитетными платежами. По графику сумма процентов составляет 34150 руб. Сколько всего выплатит Иванов?
Мое решение посчитали неправильным. На апелляции сказали, что правильный ответ 199650 руб. и проценты сложные.
Это значит, что у любого российского заемщика с кредитом аннуитетными платежами по ст. 317.1 ГК проценты НИЧТОЖНЫ.

Давайте рассмотрим поподробнее. Правильный ответ по мнению конфликтной комиссии 199650, проценты 34150. Значит, кредит был взят на сумму 199650-34150=165500.

Аннуитетный платеж со сложными процентами вычисляется по формуле:

\(165500\cdot \frac{10\%}{1-(1+10\%)^{-3}}=66550\)

Правильное решение по мнению конфликтной комиссии

год	денежный поток	погашение процентов	погашение основного долга	остаток основного долга
0	-165500			165500
1	66550	16550	50000	115500
2	66550	11550	55000	60500
3	66550	6050	60500	0
Итого:	199650	34150	165500

Здесь выдан кредит 165500, остаток основного долга в самом начале равен выданному кредиту, денежный поток вычисляется как обратный, потому что не заемщик платит банку, а банк заемщику. Поскольку банк выплатил 165500, значит денежный поток -165500.

В первый год платим аннуитетный платеж 66550, вычисленный по формуле аннуитетного платежа чуть выше. На погашение процентов ушло 165500*10%=16550. На погашение основного долга пошла вся оставшаяся от выплаты 66550 сумма 66550-16550=50000. Остаток основного долга уменьшился на сумму погашения основного долга 165500-50000=115500.

Во второй год опять платим аннуитетный платеж 66550. На погашение процентов ушло уже 115500*10%=11550. На погашение основного долга пошла вся оставшаяся от выплаты 66550 сумма 66550-11550=55000. Остаток основного долга уменьшился на сумму погашения основного долга 115500-55000=60500.

В третий год опять платим аннуитетный платеж 66550. На погашение процентов ушло уже 60500*10%=6050. На погашение основного долга пошла вся оставшаяся от выплаты 66550 сумма 66550-6050=60500. Остаток основного долга уменьшился на сумму погашения основного долга 60500-60500=0.

Проверяем, условие задачи выполнено: 16550+11550+6050=34150.

Мое решение апелляционная комиссия посчитала неправильным. Предоставляю скриншот чата с апелляционной комиссией:

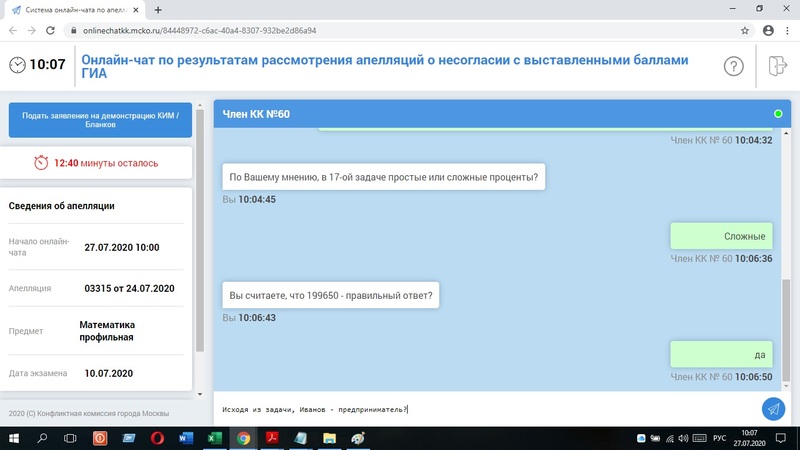Итак, получается, что У ВСЕХ заемщиков, кредит которых не связан с предпринимательской деятельностью, у которых аннуитетный платеж вычислен по формуле, близкой к 

\(A=K\cdot {i \over 1-(1+i)^{-T}}\)

, где A - аннуитетный платеж, K - выданный кредит, i - ставка за период погашения (например, за месяц), T - общее количество платежей заемщика.

условие погашения процентов - НИЧТОЖНО по п.2 ст. 317.1 ГК.

Это даже Кокорев Р.А. пишет в https://finuch.ru/lecture/8736:

в по­тре­би­тель­ском кре­ди­то­ва­нии, со­глас­но пунк­ту 2 ста­тьи 317.1 ГК РФ, слож­ные про­цен­ты ис­поль­зо­вать­ся не долж­ны.

Повторяю еще раз: если у вас есть потребительский кредит или ипотека, значит, 99.9% вероятность того, что банк вас обманул и условие начисления сложных процентов НИЧТОЖНО.

Теперь рассмотрим правильное решение данной задачи.

Для начала прочитаем этот п.2 317.1 ГК:

2. Условие обязательства, предусматривающее начисление процентов на проценты, является ничтожным, за исключением условий обязательств, возникающих из договоров банковского вклада или из договоров, связанных с осуществлением сторонами предпринимательской деятельности.

Во-первых, начисление процентов на проценты - это синонимичное выражение словам "сложные проценты".

Во-вторых, сложные проценты возможны только в том случае, если договор был заключен для предпринимательской деятельности всех сторон, участвующих в договоре.

В-третьих, ничтожен не весь договор, а только условие обязательства, предусматривающее начисление процентов на проценты.

Рассмотрим ситуацию, если кредит был выдан не целиком, а тремя частями: K1 - на срок 1 год, K2 - на срок 2 года, K3 - на срок 3 года. Причем все эти части выданы в один день. Тогда погашение этих частей кредита будет A=K1*110%=K2*120%=K3*130% (проценты простые). Действительно, K1+10%=K1+K1*10%=K1*(1+10%)=K1*110%. Сумма процентов по графикам будет K1*10%+K2*20%+K3*30%=34150

Из уравнения K1*110%=K2*120% следует, что K2=K1*110%/120%=11/12*K1

Из уравнения K1*110%=K3*130% следует, что K3=K1*110%/130%=11/13*K1

Значит, K1*10%+K2*20%+K3*30%=K1*0.1+11/12*K1*0.2+11/13*K1*0.3=419/780*K1=34150

Отсюда K1=34150*780/419=26637000/419

Следовательно, K1*110%+K2*120%+K3*130%=1.1*K1*3=87902100/419 (что и надо найти по условию задачи).

Это был бы правильный ответ, если бы возможно было выплатить 1/419 часть рубля. Поскольку это невозможно, нам надо аннуитетный платеж вычислить для каждой части кредита отдельно с точностью до копеек, а затем сложить.

Итак, первая часть кредита у нас равна 26637000/419≈63572.79

A1=63572.79*1.1≈69930.07

вторая часть кредита равна 11/12*26637000/419=24417250/419≈58275.06

A2=58275.06*1.2≈69930.07

третья часть кредита равна 11/13*26637000/419=22539000/419≈53792.36

A3=53792.36*1.3≈69930.07

Итого, ответ будет 69930.07+69930.07+69930.07=209790.21 руб.

Проверка: проценты за первую часть кредита: 69930.07-63572.79=6357.28

проценты за вторую часть кредита: 69930.07-58275.06=11655.01

проценты за третью часть кредита: 69930.07-53792.36=16137.71

Итого: 6357,28+11655.01+16137.71=34150

Теперь посмотрим, как это будет выглядеть в виде графика платежей по кредиту:

год	денежный поток	погашение процентов	погашение основного долга	остаток основного долга
0	-175640.21			175640.21
1	69930.07	6357.28	63572.79	112067.42
2	69930.07	11655.01	58275.06	53792.36
3	69930.07	16137.71	53792.36	0
Итого:	209790.21	34150	175640.21

Мы приходим к выводу, что данный расчет верный, по простым процентам, но противоречит законодательству, поскольку у нас проценты начисляются не на остаток основного долга, а на погашение основного долга. Это противоречит п.1.6 Положения 446-П "Процентные доходы и процентные расходы по размещенным и привлеченным средствам начисляются на остаток задолженности по основному долгу, учитываемой на соответствующем лицевом счете на начало операционного дня."

Следовательно, данное решение возможно только если Иванову выдали не один кредит, а три разных кредита в один день на общую сумму 175640.21, только в этом случае погашение основного долга будет равно остатку основного долга. Тогда по каждому кредиту будет свой график платежей:

год	денежный поток	погашение процентов	погашение основного долга	остаток основного долга
0	-63572.79			63572.79
1	69930.07	6357.28	63572.79	0
Итого:	69930.07	6357.28	63572.79

год	денежный поток	погашение процентов	погашение основного долга	остаток основного долга
0	-58275.06			58275.06
2	69930.07	11655.01	58275.06	0
Итого:	69930.07	11655.01	58275.06

год	денежный поток	погашение процентов	погашение основного долга	остаток основного долга
0	-53792.36			53792.36
3	69930.07	16137.71	53792.36	0
Итого:	69930.07	16137.71	53792.36

Какая же формула аннуитетного платежа простыми процентами? Пусть есть сумма кредитов K, процентная ставка за период r, требуется разделить на n аннуитетных платежей A простыми процентами.

\(K=\sum_{i=1}^nK_i\)

\(A=(1+r)K_1=(1+2r)K_2=...=(1+nr)K_n\)

\(K_i={A \over 1+ir}\)

\(K=A\sum_{i=1}^n{1 \over 1+ir}=A\sum_{i=1}^n(1+ir)^{-1}\)

\(A={K \over \sum_{i=1}^n(1+ir)^{-1}}={175640.21 \over {1\over 1.1}+{1\over 1.2}+{1\over 1.3}}\approx 69930.07\)

Сравним с формулой сложного аннуитета

\(A={K \over \sum_{i=1}^n(1+r)^{-i}}=K\cdot {r \over 1-(1+r)^{-n}}={165500\over {1\over 1.1^1}+{1\over 1.1^2}+{1\over 1.1^3}}=165500\cdot{0.1\over 1-1.1^{-3}}=66550\)

Теперь разберемся, что делать Иванову, если кредит ему выдали один, а платить надо ежегодно. Мы уже поняли, что он столкнулся с обманом, потому что ни о какой предпринимательской деятельности речь не идет. Какие будут его действия?

Через год Иванов просто не платит ни копейки, потому что кредит выдан на три года.

Разберемся, какие условия договора являются ничтожными:

1. Полная стоимость кредита. В договоре у Иванова будет указана ПСК 10% потому что i по статье 6 353-ФЗ будет вычислена по формуле

 \(-165500/(1+i)^0+66550/(1+i)^1+66550/(1+i)^2+66550/(1+i)^3=0\)

Решение этого уравнения достаточно сложное. Поэтому воспользуемся письмом ЦБ по этому поводу https://www.cbr.ru/StaticHtml/File/50624/140919.pdf

там на последней странице написано следующее:

"При расчете ПСК учитываются все платежи по кредитному договору (договору займа) (в том числе предусмотренные договором платежи в пользу третьих лиц) по принципу сложных процентов"

Итак, из апелляции нам известно, что проценты в задаче сложные, из письма ЦБ тоже известно, что ПСК рассчитывается по принципу сложных процентов, ни о каких комиссиях и прочих платежей в задаче речь не идет, значит, их нет, значит, ПСК равна процентной ставке по договору, то есть 10% годовых. Из 6 ст. 353-ФЗ "О потребкредите" нам известно, что ПСК=i*ЧБП*100. Оттуда же известно, что ЧБП - это количество платежей в год. За год у Иванова только один платеж, значит, ЧБП=1, значит, i=0.1. Проверка:

 \(-165500/(1+0.1)^0+66550/(1+0.1)^1+66550/(1+0.1)^2+66550/(1+0.1)^3=0\)

Проверка прошла успешно, значит, условие ПСК=10% ничтожно. Причем ничтожно значение ПСК как в процентах, так и в рублях.

2. Процентная ставка по договору.

Из графика платежей мы видим, что банк эту задачу решил именно таким способом, сложными процентами, как это сделал член конфликтой комиссий №60. Значит, в договоре указано 10 сложных процентов годовых, по п.2 ст. 317.1 ГК, процентная ставка ничтожна.

3. Условие в договоре, что Иванов должен каждый год платить 66550. Действительно, раз процентная ставка сложная, платеж рассчитан не простыми процентами, значит, и сам платеж ничтожен. Значит, ежегодный платеж равен нулю. Нулю не равен только один платеж, который должен быть сделан через три года, включающий полностью выплату всего долга, потому что только в этом случае погашение основного долга равно остатку основного долга по п.1.6 446-П

4. Условие в договоре, что Иванов ежегодно должен оплачивать проценты. Действительно, проценты включены в аннуитетный платеж, значит, они тоже ничтожны. Иванов должен оплатить проценты только через три года одним-единственным платежом по п.1.6 446-П.

5. Сам график платежей. График рассчитан сложными процентами с ничтожным аннуитетным платежом. Значит, сам график тоже ничтожен.

Какие условия договора остались:

1. Размер кредита. Поскольку банк посчитал именно сложными процентами, значит, размер кредита 165500 рублей остался, действительно, именно такую сумму должен был получить Иванов по задаче.

2. Срок кредита. Кредит выдан на три года, ничтожно условие ежегодного частичного погашения, а три года остается в договоре.

Итак, Иванов получил 165500 рублей на три года под ничтожную процентную ставку.

В данном случае у Иванова должны соблюдаться три основополагающих принципа: 

1. Возвратность. Иванов должен вернуть 165500 рублей

2. Платность. Иванов должен заплатить за пользование кредитом. Здесь возникает вопрос: а как он должен заплатить, если процентная ставка ничтожна? Ответ на этот вопрос дает п.1 ст. 317.1 ГК:

В случаях, когда законом или договором предусмотрено, что на сумму денежного обязательства за период пользования денежными средствами подлежат начислению проценты, размер процентов определяется действовавшей в соответствующие периоды ключевой ставкой Банка России (законные проценты), если иной размер процентов не установлен законом или договором.

На момент проведения экзамена ключевая стака Банка России составляла 4,50% годовых. Значит, за три года по состоянию на момент экзамена (поскольку мы не могли предсказать, что она поменяется) Иванов должен заплатить 4,50%*165500*3=22342.50

3. Срочность. Иванов должен вернуть 165500 рублей и заплатить 22342,50 рублей через три года, потому что срок кредитования три года.

Есть еще принципы обеспеченности и целевой использованности денежных средств. В задаче о них ничего не сказано, значит, предполагаем, что они выполнены.

Значит, за второй год Иванов также ничего не заплатит, а за третий заплатит 165500+22342.50=187842.50

Правильный ответ: Иванов через три года заплатит 187842.50 рублей