§ 20. Расчет полной стоимости кредита
В предыдущем параграфе мы рассмотрели общий метод вычисления эффективной процентной ставки для произвольной ссуды, платежи по которой совершаются актуарным способом. Сейчас мы разберём, как с помощью этого метода и простого табличного редактора найти полную стоимость кредита для актуарного способа.
Сразу спешу объяснить. Расчет полной стоимости кредита никакого отношения к математике не имеет. ЭТО ЗАКОН. С точки зрения математики - это неправильный расчет. Правильный расчет - это ЭПС. Просто я понял логику законодателя и уточнил этот расчет. Для того, чтобы определить, являются ли проценты сложными, и была введена эта функция. Если убрать все комиссии и прочие платежи, то полная стоимость кредита будет равна (или почти равна) ставке по договору. Законодатель таким образом говорит: "Проценты сложные. Вас обманывают. Они ничтожны."
Знать эту функцию нужно для того, чтобы доказать, что это сложные проценты. Вычисляете ЭПС и ПСК. Если процентная ставка почти равна или равна ЭПС - это правильные проценты, если почти равна или равна ПСК - это сложные проценты.
Если вам надо бездоказательно, не производя сложные расчеты понять, сложные это проценты или нет, то все очень просто: в графике 2 денежных потока - один отрицательный другой положительный, либо, как любит делать банк, отрицательный денежный поток скрывает, то тогда должен быть 1 платеж с погашением и процентов, и основного долга, проценты вычислены по формуле остаток основного долга*ставка*дней/365(366)/100% - значит это простые проценты. Если проценты вычислены по формуле остаток основного долга*ставка*дней/365(366)/100% и при этом в графике есть оплата процентов до последнего платежа (то есть, больше одного неотрицательного денежного потока), причем оплата процентов возможна даже при нулевом денежном потоке, - это сложные проценты. Если проценты вычислены по формуле :
остаток основного долга * ((1+ставка/100%)^(дней/365(366)-1)
то это правильные проценты.
Расчеты могут совпадать, тогда приоритет за правильными процентами.
Простые и правильные проценты не запрещены законодательно. Сложные проценты запрещены п. 2 ст. 317.1 ГК для физических лиц по кредитам и займам.
Полная стоимость кредита вычисляется по формуле ст. 6 353-ФЗ "О потребкредите", начиная с 1.09.2014 года и представляет собой устаревшее понимание сложной процентной ставки.
Актуарный метод для этих сложных процентов можно представить в виде таблицы:
|
i |
Дата |
Дата в годах |
Денеж-ный поток |
Погашение процентов |
Погашение основного долга |
Остаток основного долга |
|
0 |
d0 |
G0=G(d0) |
R0 |
|
|
K0=-R0 |
|
… |
|
|
|
|
|
|
|
i |
di |
G1=G(di) |
Ri |
Pi=Ki-1r(Gi-Gi-1) |
Hi=Ri-Pi |
Ki=Ki-1-Hi |
|
… |
|
|
|
|
|
|
|
n |
dn |
Gn=G(dn) |
Rn=Pn+Hn |
Pn=Kn-1r(Gn-Gn-1) |
Hn=Kn-1 |
Kn=0 |
Здесь:
Gi=yi+Δi/Di, где yi-год даты di, Δi - порядковый номер дня в году di, Di - продолжительность календарного года даты di. Например, G(21 сентября 2021)=2021 265/366.
r - годовая процентная ставка, например, r=10%=0,1
Пусть n=4, тогда K1=K0-H1=K0-(R1-K0r(G1-G0))=K0(1+r(G1-G0))-R1.
K2=K1-H2=K1-(R2-K1r(G2-G1))=K1(1+r(G2-G1))-R2=(K0(1+r(G1-G0))-R1)(1+r(G2-G1))-R2=K0(1+r(G1-G0))(1+r(G2-G1))-R1(1+r(G2-G1))-R2.
K3=K2-H3=K2-(R3-K2r(G3-G2))=K2(1+r(G3-G2))-R3=(K0(1+r(G1-G0))(1+r(G2-G1))-R1(1+r(G2-G1))-R2)(1+r(G3-G2))-R3=K0(1+r(G1-G0))(1+r(G2-G1))(1+r(G3-G2))-R1(1+r(G2-G1))(1+r(G3-G2))-R2(1+r(G3-G2))-R3
K4=K3-H4=K3-(R4-K3r(G4-G3))=K3(1+r(G4-G3))-R4=(K0(1+r(G1-G0))(1+r(G2-G1))(1+r(G3-G2))-R1(1+r(G2-G1))(1+r(G3-G2))-R2(1+r(G3-G2))-R3)(1+r(G4-G3))-R4=-R0(1+r(G1-G0))(1+r(G2-G1))(1+r(G3-G2))(1+r(G4-G3))-R1(1+r(G2-G1))(1+r(G3-G2))(1+r(G4-G3))-R2(1+r(G3-G2))(1+r(G4-G3))-R3(1+r(G4-G3))-R4=0
Делаем предположение для доказательства методом математической индукции:
\[K_k=-R_k-\sum_{i=0}^{k-1}R_i\prod_{j=i+1}^k(1+r(G_j-G_{j-1}))\]
1. Для k=1
\[K_1=-R_1-\sum_{i=0}^0R_i\prod_{j=1}^1(1+r(G_j-G_{j-1}))=K_0(1+r(G_1-G_0))-R_1\]
2. Если верно для k, то верно и для k+1:
\[K_{k+1}=(-R_k-\sum_{i=0}^{k-1}R_i\prod_{j=i+1}^k(1+r(G_j-G_{j-1})))(1+r(G_{k+1}-G_k))-R_{k+1}\]
Раскрываем скобку, получаем:
\[K_{k+1}=-R_{k+1}-\sum_{i=0}^kR_i\prod_{j=i+1}^{k+1}(1+r(G_j-G_{j-1}))\]
Итак, это утверждение:
\[K_{n}=-R_{n}-\sum_{i=0}^{n-1}R_i\prod_{j=i+1}^{n}(1+r(G_j-G_{j-1}))\]
доказано методом математической индукции для любого натурального n.
Отсюда, поскольку Kn=0, уравнение для r будет
\[-R_{n}-\sum_{i=0}^{n-1}R_i\prod_{j=i+1}^{n}(1+r(G_j-G_{j-1}))=0\]
Разделим обе части уравнения на \(-\prod_{j=1}^n(1+r(G_j-G{j-1}))\):
\[R_0+\sum_{i=1}^n{R_i\over \prod_{j=1}^i(1+r(G_j-G_{j-1}))}=0\]
Ответ: ПСК вычисляется из уравнения:
\[ДП_0+\sum_{i=1}^n{ДП_i\over \prod_{j=1}^i(1+{ПСК\over 100\%}\times(G_j-G_{j-1}))}=0\]
Мы получили значение ПСК, которое подразумевается в ст.6 353-ФЗ "О потребкредите"
Несмотря на то, что формула там немного другая, мы будем рассматривать именно доказанную нами формулу, поскольку вольное обращение законодателя с формулами нам уже известно:
Когда под формулой
\(S=P×(1+I×j/K)^n\)
подразумевается
\(S=P\times \prod_{k=1}^n(1+I\times(G_k-G_{k-1}))\)
Все по тому же методу Ньютона:
\[\tag{19.1} x_{(k+1)} = x_{(k)} - \frac{f(x_{(k)})}{f'(x_{(k)})},\]
находим
\[f(ПСК)=ДП_0+\sum_{i=1}^n{ДП_i\over \prod_{j=1}^i(1+{ПСК\over 100\%}\times(G_j-G_{j-1}))}\]
\[f'(ПСК)=-\sum_{i=1}^n{ДП_i\sum_{k=1}^i{G_k-G_{k-1}\over 1+{ПСК\over 100\%}\times(G_k-G_{k-1})}\over \prod_{j=1}^i(1+{ПСК\over 100\%}\times(G_j-G_{j-1}))}\]
Составляем функции на VBA Excel:
Function ДелитсяНа(ByVal y As Integer, ByVal m As Integer) As Integer
ДелитсяНа = Int(y / m) - Int((y - 1) / m)
End Function
Function ПродолжительностьГода(ByVal y As Integer) As Integer
ПродолжительностьГода = 365 + ДелитсяНа(y, 4) - ДелитсяНа(y, 100) + ДелитсяНа(y, 400)
End Function
Function ДатаВГодах(ByVal d As Date) As Double
y = Year(d)
t = ПродолжительностьГода(y)
m = Month(d)
ДатаВГодах = y - 2000 + (Day(d) + Int(30.56 * m) - 30 - Int(0.1 * m + 0.7) * (367 - t)) / t
End Function
Function ПСК(Значения As Range, Даты As Range, Optional Предп As Double = 0) As Variant
'Функция воспринимает как даты, выраженные в годах,
'так и даты excel, причем даты, выраженные в годах от 2000 года до 2366
'года воспринимаются автоматически.
'Даты 1900-го года воспринимаются, как даты, выраженные в годах
If Значения.Count <> Даты.Count Then
ПСК = "#РАЗМЕРНОСТИ ЗНАЧЕНИЙ И ДАТ НЕ СХОДЯТСЯ"
ElseIf Значения.Count = 1 Then
ПСК = "#НЕДОСТАТОЧНО ЗНАЧЕНИЙ"
Else
ПСК = Предп
ПСК0 = ПСК + 0.00001
j = 1
Dim ДатыВГодах() As Double
ReDim ДатыВГодах(Даты.Count)
If Даты(1) > 366 Then
For i = 1 To Даты.Count
ДатыВГодах(i) = ДатаВГодах(Даты(i))
Next
Else
For i = 1 To Даты.Count
ДатыВГодах(i) = Даты(i)
Next
End If
While Abs(ПСК0 - ПСК) >= 0.000000000000001 And j < 100
f = Значения(1)
diff = 0
t = 1
For i = 2 To Значения.Count
t = t * (1 + ПСК * (ДатыВГодах(i) - ДатыВГодах(i - 1)))
f = f + Значения(i) / t
df = 0
For k = 2 To i
df = df + (ДатыВГодах(k) - ДатыВГодах(k - 1)) / (1 + ПСК * (ДатыВГодах(k) - ДатыВГодах(k - 1)))
Next
diff = diff - Значения(i) * df / t
Next
ПСК0 = ПСК
ПСК = ПСК - f / diff
j = j + 1
Wend
If j = 100 Then
ПСК = "#РЯД НЕ СХОДИТСЯ:" & ПСК & ";" & ПСК0
End If
End If
End Function
Вот мы и подошли к задаче 3 "простых процентов". Чтобы точно определить, сложные это проценты или нет, надо вычислить полную стоимость кредита и, если она равна 25%, то это сложные проценты.
| Ставка | 25% | |||||
| Номер платежа | Дата | Дата в годах | Денежный поток | Погашение процентов | Погашение основного долга | Остаток основного долга |
| 0 | 01.04.2022 | 22 91/365 | -150000 | 150000 | ||
| 1 | 01.05.2022 | 22 121/365 | 3082,19 | 3082,19 | 0 | 150000 |
| 2 | 01.06.2022 | 22 152/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 3 | 01.07.2022 | 22 182/365 | 3082,19 | 3082,19 | 0 | 150000 |
| 4 | 01.08.2022 | 22 213/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 5 | 01.09.2022 | 22 244/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 6 | 01.10.2022 | 22 274/365 | 3082,19 | 3082,19 | 0 | 150000 |
| 7 | 01.11.2022 | 22 61/73 | 3184,93 | 3184,93 | 0 | 150000 |
| 8 | 01.12.2022 | 22 67/73 | 3082,19 | 3082,19 | 0 | 150000 |
| 9 | 01.01.2023 | 23 1/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 10 | 01.02.2023 | 23 32/365 | 3184,93 | 3184,93 | 0 | 150000 |
| 11 | 01.03.2023 | 23 12/73 | 2876,71 | 2876,71 | 0 | 150000 |
| 12 | 01.04.2023 | 23 91/365 | 153184,93 | 3184,93 | 150000 | 0 |
| ПСК по ст. 6 353-ФЗ: | 25,007% | |||||
| Уточненная ПСК: | 25,000% | |||||
Теперь надо проверить методом эквивалентных дисконтированных денежных потоков: разделим общий кредит 150000 на 12 неравных частей таким образом, чтобы денежные потоки совпадали:
| Номер платежа | Дата | Дата в годах | Денежный поток | Погашение процентов | Погашение основного долга | Остаток основного долга | Множители разделения на части | Денежные потоки 12 частей: | Сумма | |||||||||||
| 0 | 01.04.2022 | 22 91/365 | -150000 | 150000 | -3020,132 | -3055,918 | -2897,796 | -2932,132 | -2871,16865 | -2722,606 | -2754,8662 | -2612,321 | -2643,275 | -2588,317 | -2293,843 | -119607,61 | -150000 | |||
| 1 | 01.05.2022 | 22 121/365 | 3082,19 | 3082,19 | 0 | 150000 | 1,020548 | 3082,19 | 3082,19 | |||||||||||
| 2 | 01.06.2022 | 22 152/365 | 3184,93 | 3184,93 | 0 | 150000 | 1,042217 | 3184,93 | 3184,93 | |||||||||||
| 3 | 01.07.2022 | 22 182/365 | 3082,19 | 3082,19 | 0 | 150000 | 1,063633 | 3082,19 | 3082,19 | |||||||||||
| 4 | 01.08.2022 | 22 213/365 | 3184,93 | 3184,93 | 0 | 150000 | 1,086217 | 3184,93 | 3184,93 | |||||||||||
| 5 | 01.09.2022 | 22 244/365 | 3184,93 | 3184,93 | 0 | 150000 | 1,10928 | 3184,93 | 3184,93 | |||||||||||
| 6 | 01.10.2022 | 22 274/365 | 3082,19 | 3082,19 | 0 | 150000 | 1,132073 | 3082,19 | 3082,19 | |||||||||||
| 7 | 01.11.2022 | 22 61/73 | 3184,93 | 3184,93 | 0 | 150000 | 1,156111 | 3184,93 | 3184,93 | |||||||||||
| 8 | 01.12.2022 | 22 67/73 | 3082,19 | 3082,19 | 0 | 150000 | 1,179866 | 3082,19 | 3082,19 | |||||||||||
| 9 | 01.01.2023 | 23 1/365 | 3184,93 | 3184,93 | 0 | 150000 | 1,204918 | 3184,93 | 3184,93 | |||||||||||
| 10 | 01.02.2023 | 23 32/365 | 3184,93 | 3184,93 | 0 | 150000 | 1,230502 | 3184,93 | 3184,93 | |||||||||||
| 11 | 01.03.2023 | 23 12/73 | 2876,71 | 2876,71 | 0 | 150000 | 1,254101 | 2876,71 | 2876,71 | |||||||||||
| 12 | 01.04.2023 | 23 91/365 | 153184,93 | 3184,93 | 150000 | 0 | 1,280729 | 153184,93 | 153184,93 | |||||||||||
| ПСК по ст. 6 353-ФЗ: | 25,007% | |||||||||||||||||||
| Уточненная ПСК: | 25,000% | |||||||||||||||||||
Мы видим, что сумма всех частей равна 150000, все эти части выданы в один день, причем каждая из этих частей рассчитана по формуле сложных процентов. Причем все денежные потоки совпадают.
Например,
| Месяц | Дата | Дата в годах | Расчет долга |
| 0 | 01.04.2022 | 22 91/365 | 2932,13182 |
| 1 | 01.05.2022 | 22 121/365 | 2992,381104 |
| 2 | 01.06.2022 | 22 152/365 | 3055,917963 |
| 3 | 01.07.2022 | 22 182/365 | 3118,710798 |
| 4 | 01.08.2022 | 22 213/365 | 3184,93 |
1 апреля 2022 выдан кредит на сумму 2932,13 и погашен одним платежом 1 августа 2022 года на сумму 3184,93.
Произведем расчет сложными процентами:
\(2932,13182\cdot (1+{25\%\over 100\%}\cdot (22 121/365-22 91/365))\cdot (1+{25\%\over 100\%}\cdot (22 152/365-22 121/365))\cdot (1+{25\%\over 100\%}\cdot (22 182/365-22 152/365))\cdot (1+{25\%\over 100\%}\cdot (22 213/365-22 182/365))\approx 3184,93\)
Значит, задача 3 "простых" процентов полностью эквивалентна выдаче 12 кредитов со сложной процентной ставкой 25% годовых с ежемесячной капитализацией.
Всё, задача 3 "простых" процентов полностью доказана. Если бы все эти части рассчитывались по формуле простых процентов, то это были простые проценты, но каждая из этих частей должна быть отдельным договором.
Вот файл Excel с макросами:
http://www.antibank.su/media/1/IRR.xlsm
Вот подтверждение, что это сложные проценты:
https://www.cbr.ru/Content/Document/File/104862/140919.pdf
Там на последней странице указано:
"При расчете ПСК учитываются все платежи по кредитному договору ... по принципу сложных процентов"
Пример
Кредит размером 24 тысячи евро, выданный 1.09.2020 на два года под 12% годовых, погашается ежемесячными платежами в соответствии с дифференцированной схемой. Комиссия за организацию кредита составляет 1% от его суммы. Кроме того, каждый месяц с заёмщика взимается комиссия за ведение ссудного счёта размером 0,1% от суммы кредита. Проценты вычисляются по устаревшим правилам сложных процентов. Нам нужно найти полную стоимость кредита.
Прежде всего, построим график погашения кредита.
При получении кредита заёмщик был вынужден заплатить 0,01 · 24 000 = 240 евро, а каждый месяц с него взимается комиссия размером 0,001 · 24 000 = 24 евро. Значит, график платежей по кредиту имеет следующий вид:
| Дата | Дата в годах | Денежный поток | Погашение процентов | Погашение основного долга | Комиссии и прочие платежи | Остаток основного долга |
| 01.09.2020 | 20 245/366 | -23760 | 240 | 24000 | ||
| 01.10.2020 | 20 275/366 | 1496,13 | 472,13 | 1000 | 24 | 23000 |
| 01.11.2020 | 20 51/61 | 1491,54 | 467,54 | 1000 | 24 | 22000 |
| 01.12.2020 | 20 56/61 | 1456,79 | 432,79 | 1000 | 24 | 21000 |
| 01.01.2021 | 21 1/365 | 1450,92 | 426,92 | 1000 | 24 | 20000 |
| 01.02.2021 | 21 32/365 | 1431,67 | 407,67 | 1000 | 24 | 19000 |
| 01.03.2021 | 21 12/73 | 1373,81 | 349,81 | 1000 | 24 | 18000 |
| 01.04.2021 | 21 91/365 | 1390,9 | 366,9 | 1000 | 24 | 17000 |
| 01.05.2021 | 21 121/365 | 1359,34 | 335,34 | 1000 | 24 | 16000 |
| 01.06.2021 | 21 152/365 | 1350,14 | 326,14 | 1000 | 24 | 15000 |
| 01.07.2021 | 21 182/365 | 1319,89 | 295,89 | 1000 | 24 | 14000 |
| 01.08.2021 | 21 213/365 | 1309,37 | 285,37 | 1000 | 24 | 13000 |
| 01.09.2021 | 21 244/365 | 1288,99 | 264,99 | 1000 | 24 | 12000 |
| 01.10.2021 | 21 274/365 | 1260,71 | 236,71 | 1000 | 24 | 11000 |
| 01.11.2021 | 21 61/73 | 1248,22 | 224,22 | 1000 | 24 | 10000 |
| 01.12.2021 | 21 67/73 | 1221,26 | 197,26 | 1000 | 24 | 9000 |
| 01.01.2022 | 22 1/365 | 1207,45 | 183,45 | 1000 | 24 | 8000 |
| 01.02.2022 | 22 32/365 | 1187,07 | 163,07 | 1000 | 24 | 7000 |
| 01.03.2022 | 22 12/73 | 1152,88 | 128,88 | 1000 | 24 | 6000 |
| 01.04.2022 | 22 91/365 | 1146,3 | 122,3 | 1000 | 24 | 5000 |
| 01.05.2022 | 22 121/365 | 1122,63 | 98,63 | 1000 | 24 | 4000 |
| 01.06.2022 | 22 152/365 | 1105,53 | 81,53 | 1000 | 24 | 3000 |
| 01.07.2022 | 22 182/365 | 1083,18 | 59,18 | 1000 | 24 | 2000 |
| 01.08.2022 | 22 213/365 | 1064,77 | 40,77 | 1000 | 24 | 1000 |
| 01.09.2022 | 22 244/365 | 1044,38 | 20,38 | 1000 | 24 | 0 |
Теперь рассчитаем полную стоимость кредита при помощи полученной нами функции ПСК:
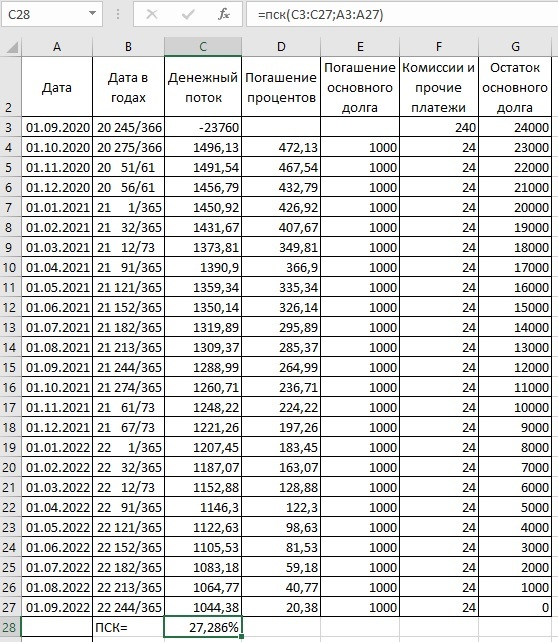
Мы получили ПСК отличную от 24% в силу того, что комиссии и прочие платежи не равны 0
Для сравнения посмотрим, как будет считать встроенная функция ВСД:
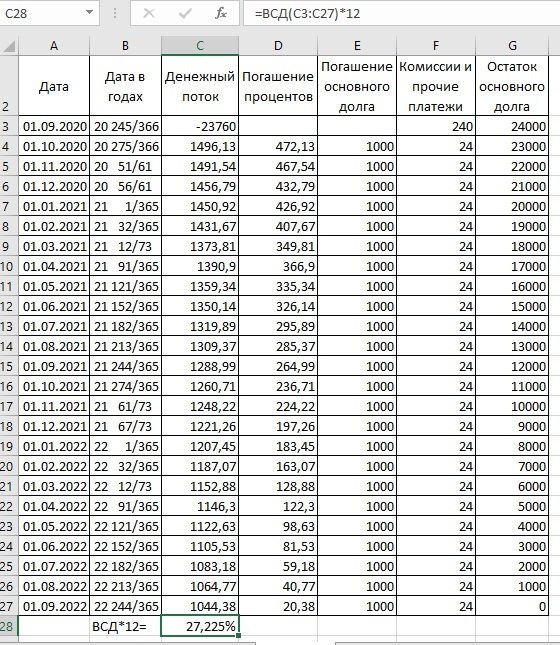
Мы видим, что функция ВСД считает неточно (27,225% против 27,286%)