На протяжении двух предыдущих параграфов мы рассматривали общие методы, с помощью которых можно определить эффективную процентную ставку и полную стоимость кредита для произвольной ссуды.

Разберем пример из предыдущего параграфа при нулевых комиссиях:

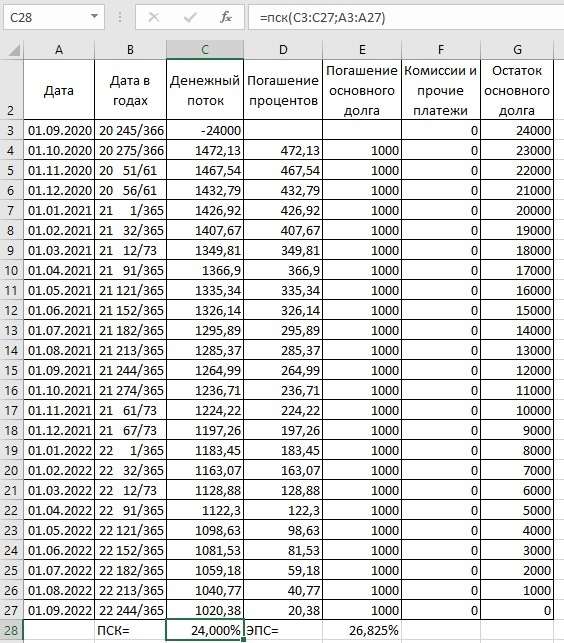
Итак, мы видим, что какой бы ни был кредит с актуарным методом и с устаревшим расчетом сложных процентов, ПСК всегда равна номинальной ставке по договору, если все комиссии равны 0. Это было доказано в предыдущем параграфе методом математической индукции. ЭПС при этом примерно равна

\(ЭПС\approx ((1+{ПСК\over ЧБП\times 100\%})^{ЧБП}-1) \times 100\%=((1+{24\%\over 12\times 100\%})^{12}-1)\times 100\%\approx 26,824\%\)

ЧБП - это число базовых периодов в год, то есть, период капитализации, в данном случае это 12.

Рассмотрим теперь пример предыдущего параграфа с нулевыми комиссиями при расчете правильными процентами:

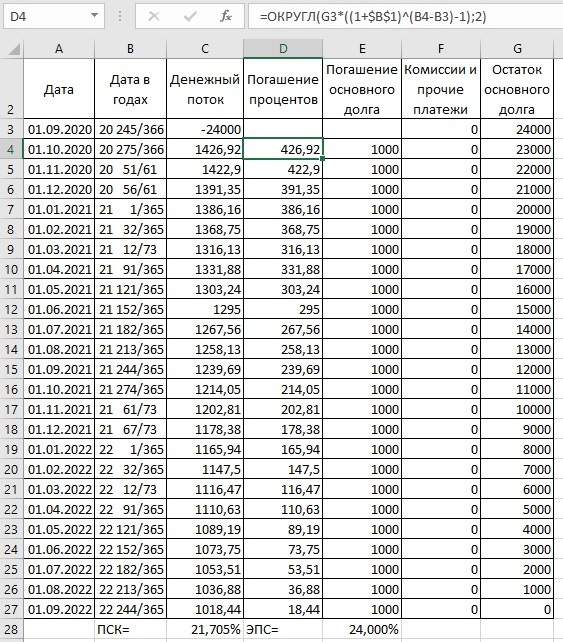
Все так же: каким бы ни был кредит с актуарным методом и правильными процентами, эффективная процентная ставка всегда равна номинальной ставке по договору при отсутствии комиссий и прочих платежей. Это доказывается идентично ПСК (в предыдущем параграфе) методом математической индукции. ПСК при этом примерно равна:

\(ПСК\approx \left(\sqrt[ЧБП]{1+{ЭПС\over 100\%}}-1\right)\times ЧБП\times 100\% =\left(\sqrt[12]{1+{24\%\over 100\%}}-1\right)\times 12\times 100\%\approx 21,705\%\)

Докажем методом математической индукции, что эффективная процентная ставка всегда равна номинальной ставке по договору при отсутствии комиссий и прочих платежей.

Актуарный метод для правильных сложных процентов можно представить в виде таблицы:

i	Дата	Дата в годах	Денеж-ный поток	Погашение процентов	Погашение основного долга	Остаток основного долга
0	d0	G0=G(d0)	R0			K0=-R0
…
i	di	G1=G(di)	Ri	\(P_i=K_{i-1}\cdot ((1+r)^{G_i-G_{i-1}}-1)\)	Hi=Ri-Pi	Ki=Ki-1-Hi
…
n	dn	Gn=G(dn)	Rn=Pn+Hn	\(P_n=K_{n-1}\cdot ((1+r)^{G_n-G_{n-1}}-1)\)	Hn=Kn-1	Kn=0

Здесь:

G_i=y_i+Δ_i/D_i, где y_i-год даты d_i, Δ_i - порядковый номер дня в году d_i, D_i - продолжительность календарного года даты d_i. Например, G(21 сентября 2021)=2021 265/366.

r - годовая процентная ставка, например, r=10%=0,1

Пусть n=4, тогда \(K_1=K_0-H_1=K_0-(R_1-K_0\cdot ((1+r)^{G_1-G_0}-1))=K_0\cdot (1+r)^{G_1-G_0}-R_1\)

\(K_2=K_1-H_2=K_1-(R_2-K_1\cdot((1+r)^{G_2-G_1}-1))=K_1\cdot(1+r)^{G_2-G_1}-R_2\)

\(K_2=(K_0\cdot (1+r)^{G_1-G_0}-R_1)\cdot(1+r)^{G_2-G_1}-R_2=K_0\cdot(1+r)^{G_2-G_0}-R_1\cdot(1+r)^{G_2-G_1}-R_2\)

\(K_3=K_2-H_3=K_2-(R_3-K_2\cdot((1+r)^{G_3-G_2}-1))=K_2\cdot(1+r)^{G_3-G_2}-R_3\)

\(K_3=(K_0\cdot(1+r)^{G_2-G_0}-R_1\cdot(1+r)^{G_2-G_1}-R_2)\cdot(1+r)^{G_3-G_2}-R_3\)

\(K_3=K_0\cdot(1+r)^{G_3-G_0}-R_1\cdot(1+r)^{G_3-G_1}-R_2\cdot(1+r)^{G_3-G_2}-R_3\)

\(K_4=K_3-H_4=K_3-(R_4-K_3\cdot((1+r)^{G_4-G_3}-1))=K_3\cdot(1+r)^{G_4-G_3}-R_4\)

\(K_4=(K_0\cdot(1+r)^{G_3-G_0}-R_1\cdot(1+r)^{G_3-G_1}-R_2\cdot(1+r)^{G_3-G_2}-R_3)\cdot(1+r)^{G_4-G_3}-R_4\)

\(K_4=K_0\cdot(1+r)^{G_4-G_0}-R_1\cdot(1+r)^{G_4-G_1}-R_2\cdot(1+r)^{G_4-G_2}-R_3\cdot(1+r)^{G_4-G_3}-R_4\)

Делаем предположение для доказательства методом математической индукции:

\[K_k=-\sum_{i=0}^{k}R_i(1+r)^{G_k-G_i}\]

1. Для k=1

\[K_1=-\sum_{i=0}^1R_i(1+r)^{G_1-G_i}=K_0(1+r)^{G_1-G_0}-R_1\]

2. Если верно для k, то верно и для k+1:

\[K_{k+1}=K_k\cdot(1+r)^{G_{k+1}-G_k}-R_{k+1}\]

Раскрываем K_k, получаем:

\[K_{k+1}=-(1+r)^{G_{k+1}-G_k}\cdot\sum_{i=0}^{k}R_i(1+r)^{G_k-G_i}-R_{k+1}\]

\[K_{k+1}=-\sum_{i=0}^{k+1}R_i(1+r)^{G_{k+1}-G_i}\]

Итак, это утверждение:

\[K_n=-\sum_{i=0}^{n}R_i(1+r)^{G_n-G_i}\]

доказано методом математической индукции для любого натурального n.

Отсюда, поскольку K_n=0, уравнение для r будет

\[K_n=-\sum_{i=0}^{n}R_i(1+r)^{G_n-G_i}=0\]

Разделим обе части уравнения на \(-(1+r)^{G_n-G_0}\):

\[\sum_{i=0}^{n}{R_i\over(1+r)^{G_i-G_0}}=0\]

Ответ: ПСК вычисляется из уравнения:

\[\sum_{i=0}^{n}{ДП_i\over(1+{ПСК\over 100\%})^{G_i-G_0}}=0\]

И ещё одно общее замечание относительно выбора численного метода. Существует великое множество численных методов, многие из которых вполне можно было бы применить для решения наших задач. Метод Ньютона был выбран из-за его, на мой взгляд, оптимального соотношения между сложностью применения и скоростью сходимости (вы ведь помните, мы ни в одном из примеров не делали больше восьми итераций). Существуют более быстрые, но более сложные для понимания методы. Существуют более простые методы, с меньшим количеством ограничений и гарантированной сходимостью, но требующие большого количества вычислений. Например, если бы мы в последнем примере использовали широко известный метод простой итерации, то для достижения требуемой точности нам пришлось бы сделать около сотни вычислений. Понятно, что эти вычисления делает программа, но тем не менее.